报告题目:The extremal average distance of cubic graphs
报告人:张晓东 教授 上海交通大学
照片:

报告时间:2023年10月11日下午14:30-17:30
腾讯会议:343-329-208
报告人简介:
张晓东,上海交通大学数学科学公司教授、博士生导师。1998年6月在中国科学技术大学获得理学博士学位。曾在以色列理工公司(得到Lady Davis Postdoctoral fellowship资助)和智利大学做博士后、在美国加州大学圣地亚哥分校等校做访问学者。多次主持和参加国家自然科学基金项目。 目前主要研究领域谱图理论、极值图论, 随机图与复杂网络,组合矩阵论等。
报告摘要: The average distance
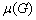 of a simple connected graph
of a simple connected graph
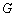 is the average of the distances between all pairs of vertices in
is the average of the distances between all pairs of vertices in
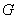 . We prove that for a connected cubic graph
. We prove that for a connected cubic graph
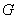 on
on
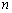 vertices,
vertices,
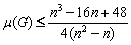 , if
, if
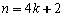 ; and
; and
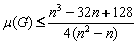 , if
, if
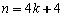 . Furthermore, all extremal graphs attaining the upper bounds are characterized, and they have the maximum possible diameter. The result solves a question of
. Furthermore, all extremal graphs attaining the upper bounds are characterized, and they have the maximum possible diameter. The result solves a question of
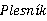 and proves a conjecture of
and proves a conjecture of
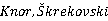 and
and
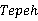 on the average distance of cubic graphs. The proofs use graph transformations and structural graph analysis. This talk is joined with Yi-Ze Chen, Xin Li (Shanghai Jiao Tong University).
on the average distance of cubic graphs. The proofs use graph transformations and structural graph analysis. This talk is joined with Yi-Ze Chen, Xin Li (Shanghai Jiao Tong University).
